clear
UNESP 2014/1
Uma pessoa está parada numa calçada plana e horizontal diante de um espelho plano vertical E pendurado na fachada de uma loja. A figura representa a visão de cima da região.
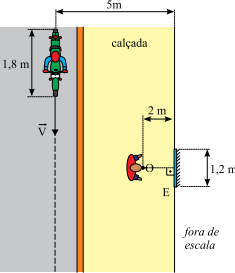
Olhando para o espelho, a pessoa pode ver a imagem de um motociclista e de sua motocicleta que passam pela rua com velocidade constante V = 0,8 m/s, em uma trajetória retilínea paralela à calçada, conforme indica a linha tracejada.
Considerando que o ponto O na figura represente a posição dos olhos da pessoa parada na calçada, é correto afirmar que ela poderá ver a imagem por inteiro do motociclista e de sua motocicleta refletida no espelho durante um intervalo de tempo, em segundos, igual a
a
2.
b
3.
c
4.
d
5.
e
1.
Ver resposta
Ver resposta
Resposta
B
Resolução
Assine a AIO para ter acesso a esta e muitas outras resoluções
Mais de 300.000 questões com resoluções e dados exclusivos disponíveis para alunos AIO.
E mais: nota TRI a todo o momento.
E mais: nota TRI a todo o momento.
Saiba mais
Esta resolução não é pública. Assine a aio para ter acesso a essa resolução e muito mais:
Tenha acesso a simulados reduzidos, mais de 200.000 questões, orientação personalizada,
video aulas, correção de redações e uma equipe sempre disposta a te ajudar.
Tudo isso com acompanhamento TRI em tempo real.
Dicas
expand_more
expand_less
Dicas sobre como resolver essa questão
Erros Comuns
expand_more
expand_less
Alguns erros comuns que estudantes podem cometer ao resolver esta questão
Conceitos chave
Conceitos chave sobre essa questão, que pode te ajudar a resolver questões similares
Estratégia de resolução
Uma estratégia sobre a forma apropriada de se chegar a resposta correta
Transforme seus estudos com a AIO!
Estudantes como você estão acelerando suas aprovações usando nossa plataforma de
AI + aprendizado ativo.
+25 pts
Aumento médio TRI
4x
Simulados mais rápidos
+50 mil
Estudantes

Murilo Martins
Com a ajuda da AIO, aumentei os meus acertos nos simulados e no ENEM, além de garantia uma TRI mais elevada. Recomendo a AIO para estudantes de todo nível, sendo uma maneira de alavancar a sua nota no menor tempo possível!

Jonas de Souza
As correções de redações e as aulas são bem organizadas e é claro os professores são os melhores com a melhor metodologia de ensino, sem dúvidas contribuiu muito para o aumento de 120 pontos na minha média final!

Tom
A AIO foi essencial na minha preparação porque me auxiliou a pular etapas e estudar aquilo que eu realmente precisava no momento. Eu gostava muito de ter uma ideia de qual era a minha nota TRI, pois com isso eu ficava por dentro se estava evoluindo ou não


