clear
ENEM 2021 segunda aplicação
Uma indústria recortou uma placa de metal no formato triangular ABC, conforme Figura 1, com lados 18,14e 12cm.
Posteriormente, a peça triangular ABC foi dobrada, de tal maneira que o vértice B ficou sobre o segmento AC, e o segmento DE ficou paralelo ao lado AC, conforme Figura 2.
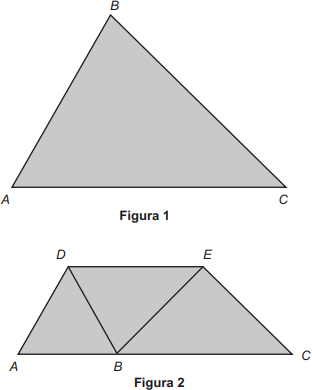
Sabe-se que, na Figura 1, o ângulo ACB é menor que o ângulo CÂB e este é menor que o ângulo ABC, e que os cortes e dobraduras foram executados corretamente pelas máquinas.
Nessas condições, qual é o valor da soma dos comprimentos, em centímetro, dos segmentos DB, BE e EC?
a
19
b
20
c
21
d
23
e
24
Ver resposta
Ver resposta
Resposta
B
Tempo médio
2 min
Resolução
Assine a AIO para ter acesso a esta e muitas outras resoluções
Mais de 300.000 questões com resoluções e dados exclusivos disponíveis para alunos AIO.
E mais: nota TRI a todo o momento.
E mais: nota TRI a todo o momento.
Saiba mais
Esta resolução não é pública. Assine a aio para ter acesso a essa resolução e muito mais:
Tenha acesso a simulados reduzidos, mais de 200.000 questões, orientação personalizada,
video aulas, correção de redações e uma equipe sempre disposta a te ajudar.
Tudo isso com acompanhamento TRI em tempo real.
Dicas
expand_more
expand_less
Dicas sobre como resolver essa questão
Erros Comuns
expand_more
expand_less
Alguns erros comuns que estudantes podem cometer ao resolver esta questão
Conceitos chave
Conceitos chave sobre essa questão, que pode te ajudar a resolver questões similares
Estratégia de resolução
Uma estratégia sobre a forma apropriada de se chegar a resposta correta
23%
Taxa de acerto
11.1
Média de pontos TRI
Habilidade
Resolver situação-problema que envolva conhecimentos geométricos de espaço e forma.
Porcentagem de alternativa escolhida por nota TRI
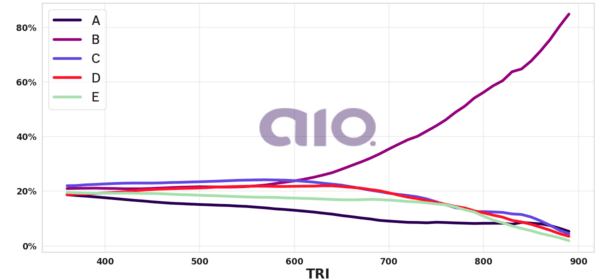
Porcentagem de alternativa escolhida por nota TRI

Transforme seus estudos com a AIO!
Estudantes como você estão acelerando suas aprovações usando nossa plataforma de
AI + aprendizado ativo.
+25 pts
Aumento médio TRI
4x
Simulados mais rápidos
+50 mil
Estudantes

Jefferson, formando em Medicina
Com a plataforma AIO consegui acertar as 45 questões de ciências humanas no ENEM 2022! Sem dúvidas, obter a nota máxima nessa área, foi imprescindível para ser aprovado em medicina.

Débora Adelina
O que mais gostei foi a forma como a plataforma seleciona matérias em que tenho mais dificuldade, ajudando a focar no que realmente preciso de atenção. Ainda não consegui minha aprovação, mas contarei com a AIO por mais um ano pois a plataforma me aproximou desse objetivo tornando meus estudos mais direcionados!

Joice Neves
Faltavam 3 meses para o ENEM, eu estava desesperada e mentalmente fragilizada por não ver os resultados do meu esforço. Então, eu encontrei a AIO e, em 3 meses, eu consegui aumentar a minha nota média em 50 pontos. Meses depois, fui aprovada no curso que eu tanto desejei. Esse sonho se tornou real graças à AIO.


