ENEM 2018 segunda aplicação
Uma indústria automobilística está testando um novo modelo de carro. Cinquenta litros de combustível são colocados no tanque desse carro, que é dirigido em uma pista de testes até que todo o combustível tenha sido consumido. O segmento de reta no gráfico mostra o resultado desse teste, no qual a quantidade de combustível no tanque é indicada no eixo y (vertical), e a distância percorrida pelo automóvel é indicada no eixo x (horizontal).
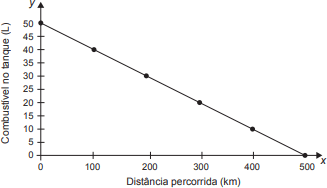
A expressão algébrica que relaciona a quantidade de combustível no tanque e a distância percorrida pelo automóvel é
y = -10x + 500
\(y = \frac{-x}{10} + 50\)
\( y = \frac{-x}{10} + 500 \)
\( y = \frac{x}{10} + 50 \)
\( y = \frac{x}{10} + 500 \)
Resolução
A questão pede para encontrar a expressão algébrica que relaciona a quantidade de combustível no tanque (y) e a distância percorrida (x), com base no gráfico fornecido. O gráfico representa uma reta, o que indica uma relação linear entre as variáveis, descrita pela equação geral da reta: \(y = mx + b\), onde \(m\) é o coeficiente angular (inclinação da reta) e \(b\) é o coeficiente linear (o ponto onde a reta intercepta o eixo y).
Passo 1: Identificar o coeficiente linear (b)
O coeficiente linear \(b\) é o valor de \(y\) quando \(x = 0\). Observando o gráfico, vemos que a reta intercepta o eixo \(y\) (Combustível no tanque) no ponto (0, 50). Portanto, \(b = 50\).
Passo 2: Identificar o coeficiente angular (m)
O coeficiente angular \(m\) representa a taxa de variação de \(y\) em relação a \(x\), ou seja, a inclinação da reta. Podemos calculá-lo usando dois pontos quaisquer da reta. Já temos o ponto (0, 50). Outro ponto claramente indicado no gráfico é onde o combustível acaba (\(y = 0\)), que ocorre quando a distância percorrida é \(x = 500\) km. Este é o ponto (500, 0).
A fórmula para o coeficiente angular \(m\) usando dois pontos \((x_1, y_1)\) e \((x_2, y_2)\) é:
\[m = \frac{y_2 - y_1}{x_2 - x_1}\]Usando os pontos (0, 50) e (500, 0):
\[m = \frac{0 - 50}{500 - 0} = \frac{-50}{500}\]Simplificando a fração:
\[m = -\frac{50}{500} = -\frac{1}{10}\]O coeficiente angular é \(m = -1/10\). Isso significa que para cada 10 km percorridos, o carro consome 1 litro de combustível (o sinal negativo indica que a quantidade de combustível diminui à medida que a distância aumenta).
Passo 3: Escrever a equação da reta
Agora que temos o coeficiente angular \(m = -1/10\) e o coeficiente linear \(b = 50\), podemos substituir esses valores na equação geral da reta \(y = mx + b\):
\[y = \left(-\frac{1}{10}\right)x + 50\]Essa equação pode ser escrita como:
\[y = -\frac{x}{10} + 50\]Passo 4: Comparar com as alternativas
Comparando a equação encontrada com as alternativas fornecidas:
- A: y = -10x + 500 (Incorreta)
- B: \(y = \frac{-x}{10} + 50\) (Correta)
- C: \( y = \frac{-x}{10} + 500 \) (Incorreta)
- D: \( y = \frac{x}{10} + 50 \) (Incorreta)
- E: \( y = \frac{x}{10} + 500 \) (Incorreta)
A alternativa correta é a B.
Dicas
Erros Comuns
Para resolver esta questão, é fundamental compreender o conceito de Função Afim (ou Função do 1º Grau) e sua representação gráfica.
Uma função afim é definida pela fórmula \(f(x) = ax + b\) ou \(y = mx + b\), onde:
- \(x\) é a variável independente (neste caso, a distância percorrida).
- \(y\) (ou \(f(x)\)) é a variável dependente (neste caso, a quantidade de combustível).
- \(m\) (ou \(a\)) é o coeficiente angular: representa a taxa de variação de \(y\) em relação a \(x\). Graficamente, é a inclinação da reta. Pode ser calculado por \(m = \frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2 - x_1}\), usando dois pontos \((x_1, y_1)\) e \((x_2, y_2)\) da reta. Se \(m > 0\), a reta é crescente; se \(m < 0\), a reta é decrescente; se \(m = 0\), a reta é horizontal.
- \(b\) é o coeficiente linear: representa o valor de \(y\) quando \(x = 0\). Graficamente, é o ponto onde a reta intercepta o eixo \(y\).
A representação gráfica de uma função afim é sempre uma reta.
Interpretar gráfico cartesiano que represente relações entre grandezas.





