clear
ENEM 2018 segunda aplicação
Um projétil é lançado por um canhão e atinge o solo a uma distância de 150 metros do ponto de partida. Ele percorre uma trajetória parabólica, e a altura máxima que atinge em relação ao solo é de 25 metros.
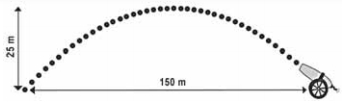
Admita um sistema de coordenadas xy em que no eixo vertical y está representada a altura e no eixo horizontal x está representada a distância, ambas em metro. Considere que o canhão está no ponto (150; 0) e que o projétil atinge o solo no ponto (0; 0) do plano xy. A equação da parábola que representa a trajetória descrita pelo projétil é
a
y = 150x - x2
b
y = 3750x - 25x2
c
75y = 300x - 2x2
d
125y = 450x - 3x2
e
225y = 150x - x2
Ver resposta
Transforme seus estudos com a AIO!
Estudantes como você estão acelerando suas aprovações usando nossa plataforma de
AI + aprendizado ativo.
+25 pts
Aumento médio TRI
4x
Simulados mais rápidos
+50 mil
Estudantes

Mariana Scheffel
AIO foi fundamental para a evolução do meu número de acertos e notas, tanto no ENEM quanto em outros vestibulares, fornecendo os recursos e as ferramentas necessárias para estudar de forma eficaz e melhorar minhas notas.

Sarah
Neste ano da minha aprovação, a AIO foi a forma perfeita de eu entender meus pontos fortes e fracos, melhorar minha estratégia de prova e, alcançar uma nota excepcional que me permitiu realizar meu objetivo na universidade dos meus sonhos. Só tenho a agradecer à AIO ... pois com certeza não conseguiria sozinha.

Tom
A AIO foi essencial na minha preparação porque me auxiliou a pular etapas e estudar aquilo que eu realmente precisava no momento. Eu gostava muito de ter uma ideia de qual era a minha nota TRI, pois com isso eu ficava por dentro se estava evoluindo ou não


