EEAR 2020/2
Um jogador de basquete lança manualmente de uma altura “h” uma bola com uma velocidade de módulo igual a v0 e com um ângulo em relação a horizontal igual a θ, conforme o desenho. No mesmo instante, o jogador sai do repouso e inicia um movimento horizontal, retilíneo uniformemente variado até a posição final xF , conforme o desenho.
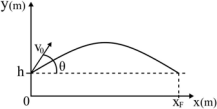
Considere que, durante todo o deslocamento, a bola não sofre nenhum tipo de atrito e que nesse local atua uma gravidade de módulo igual a “g”.
A aceleração horizontal necessária que o jogador deve ter para alcançar a bola quando a mesma retorna a altura de lançamento “h” com a qual iniciou, é corretamente expressa por ____.
\(\frac{2v_0^2}{X_F}\)
\(\frac{2v__0 cos\theta}{X_F}\)
\(\frac{v_0^2cos^2\theta}{X_F}\)
\(\frac{2v_0^2cos^2\theta}{X_F}\)
E mais: nota TRI a todo o momento.





