clear
ENEM 2017
Um garçom precisa escolher uma bandeja de base retangular para servir quatro taças de espumante que precisam ser dispostas em uma única fileira, paralela ao lado maior da bandeja, e com suas bases totalmente apoiadas na bandeja. A base e a borda superior das taças são círculos de raio 4 cm e 5 cm, respectivamente.

A bandeja a ser escolhida deverá ter uma área mínima, em centímetro quadrado, igual a
a
192.
b
300.
c
304.
d
320.
e
400.
Ver resposta
Ver resposta
Resposta
C
Tempo médio
2 min
Resolução
Assine a AIO para ter acesso a esta e muitas outras resoluções
Mais de 300.000 questões com resoluções e dados exclusivos disponíveis para alunos AIO.
E mais: nota TRI a todo o momento.
E mais: nota TRI a todo o momento.
Saiba mais
Esta resolução não é pública. Assine a aio para ter acesso a essa resolução e muito mais:
Tenha acesso a simulados reduzidos, mais de 200.000 questões, orientação personalizada,
video aulas, correção de redações e uma equipe sempre disposta a te ajudar.
Tudo isso com acompanhamento TRI em tempo real.
Dicas
expand_more
expand_less
Dicas sobre como resolver essa questão
Erros Comuns
expand_more
expand_less
Alguns erros comuns que estudantes podem cometer ao resolver esta questão
Conceitos chave
Conceitos chave sobre essa questão, que pode te ajudar a resolver questões similares
Estratégia de resolução
Uma estratégia sobre a forma apropriada de se chegar a resposta correta
13%
Taxa de acerto
0.5
Média de pontos TRI
Habilidade
Resolver situação-problema que envolva medidas de grandezas.
Porcentagem de alternativa escolhida por nota TRI
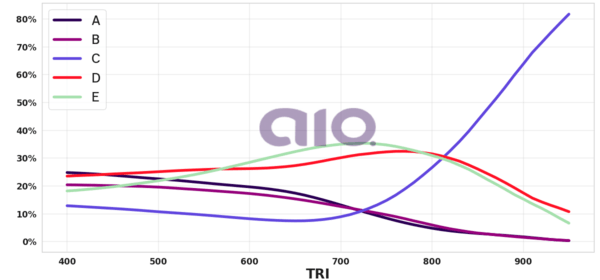
Porcentagem de alternativa escolhida por nota TRI

Transforme seus estudos com a AIO!
Estudantes como você estão acelerando suas aprovações usando nossa plataforma de
AI + aprendizado ativo.
+25 pts
Aumento médio TRI
4x
Simulados mais rápidos
+50 mil
Estudantes

Sarah
Neste ano da minha aprovação, a AIO foi a forma perfeita de eu entender meus pontos fortes e fracos, melhorar minha estratégia de prova e, alcançar uma nota excepcional que me permitiu realizar meu objetivo na universidade dos meus sonhos. Só tenho a agradecer à AIO ... pois com certeza não conseguiria sozinha.

Jefferson, formando em Medicina
Com a plataforma AIO consegui acertar as 45 questões de ciências humanas no ENEM 2022! Sem dúvidas, obter a nota máxima nessa área, foi imprescindível para ser aprovado em medicina.

Jonas de Souza
As correções de redações e as aulas são bem organizadas e é claro os professores são os melhores com a melhor metodologia de ensino, sem dúvidas contribuiu muito para o aumento de 120 pontos na minha média final!


