ENEM 2018 segunda aplicação
Um brinquedo chamado pula-pula, quando visto de cima, consiste de uma cama elástica com contorno em formato de um hexágono regular.
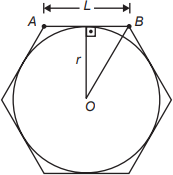
Se a área do círculo inscrito no hexágono é 3
metros quadrados, então a área do hexágono, em metro quadrado, é
9
\(6\sqrt{3}\)
\(9\sqrt{2}\)
12
\(12\sqrt{3}\)
Resolução
Passo a passo da solução:
-
Identificar a informação dada: A área do círculo inscrito no hexágono regular é \(3\pi\) metros quadrados.
-
Usar a fórmula da área do círculo: A fórmula da área de um círculo é \(A_{círculo} = \pi r^2\), onde \(r\) é o raio.
Sabemos que \(A_{círculo} = 3\pi\). Então, temos a equação:
\[ \pi r^2 = 3\pi \] -
Calcular o raio do círculo inscrito: Dividindo ambos os lados da equação por \(\pi\), obtemos:
\[ r^2 = 3 \]Portanto, o raio do círculo inscrito é \(r = \sqrt{3}\) metros (o raio deve ser positivo).
-
Relacionar o raio do círculo inscrito com o hexágono: O raio \(r\) do círculo inscrito em um polígono regular é igual ao apótema (a) desse polígono. Logo, o apótema do hexágono é \(a = r = \sqrt{3}\) metros.
-
Calcular a área do hexágono regular: A área de um hexágono regular pode ser calculada de algumas formas. Uma delas relaciona a área diretamente com o apótema (\(a\) ou \(r\) neste caso):
\[ A_{hexágono} = 2\sqrt{3} a^2 \]Substituindo \(a = \sqrt{3}\) (ou \(a^2 = 3\)), temos:
\[ A_{hexágono} = 2\sqrt{3} \times 3 \] \[ A_{hexágono} = 6\sqrt{3} \text{ metros quadrados} \] -
Método alternativo (usando o lado L):
a. Relacionar o apótema \(a\) com o lado \(L\) do hexágono regular: \(a = \frac{L\sqrt{3}}{2}\).
b. Substituir \(a = \sqrt{3}\): \(\sqrt{3} = \frac{L\sqrt{3}}{2}\).
c. Resolver para \(L\): Dividindo por \(\sqrt{3}\), temos \(1 = \frac{L}{2}\), o que implica \(L = 2\) metros.
d. Calcular a área do hexágono usando a fórmula com o lado \(L\): \(A_{hexágono} = \frac{3L^2\sqrt{3}}{2}\).
e. Substituir \(L = 2\): \(A_{hexágono} = \frac{3(2^2)\sqrt{3}}{2} = \frac{3(4)\sqrt{3}}{2} = \frac{12\sqrt{3}}{2} = 6\sqrt{3}\) metros quadrados.
-
Conclusão: Ambos os métodos confirmam que a área do hexágono regular é \(6\sqrt{3}\) metros quadrados.
Dicas
Erros Comuns
Revisão de Conceitos
- Área do Círculo: A área de um círculo de raio \(r\) é dada pela fórmula \(A = \pi r^2\).
- Hexágono Regular: Um polígono com 6 lados e 6 ângulos internos iguais. Pode ser decomposto em 6 triângulos equiláteros congruentes com um vértice comum no centro do hexágono.
- Círculo Inscrito: Um círculo é inscrito em um polígono se ele tangencia todos os lados do polígono. O raio desse círculo é chamado de apótema do polígono.
- Apótema (a) de um Hexágono Regular: É a distância do centro do hexágono ao ponto médio de um lado. Corresponde à altura de um dos 6 triângulos equiláteros que compõem o hexágono. Se \(L\) é o lado do hexágono, \(a = \frac{L\sqrt{3}}{2}\).
- Área do Hexágono Regular: Pode ser calculada como 6 vezes a área de um dos triângulos equiláteros (\(A = 6 \times \frac{L^2\sqrt{3}}{4} = \frac{3L^2\sqrt{3}}{2}\)) ou usando o apótema \(a\) e o perímetro \(P=6L\) (\(A = \frac{P \times a}{2} = \frac{6L \times a}{2} = 3La\)). Também pode ser expressa apenas em função do apótema: \(A = 2\sqrt{3}a^2\).
Resolver situação-problema que envolva conhecimentos geométricos de espaço e forma.
