UEA Geral 2018
Um barco está atracado em uma das margens de um rio e de dentro dele um garoto bate com uma haste na água, produzindo ondas planas que se propagam na superfície do rio. O leito desse rio apresenta duas regiões com profundidades diferentes, \(h_1\) e \(h_2 ,\) e, quando uma onda refrata de uma região para outra, seu comprimento de onda se altera de \(\lambda_1\) para \(\lambda_2.\)
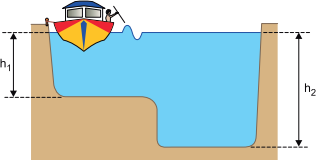
Considerando que a velocidade de propagação de uma onda na superfície de um líquido de profundidade h pode ser calculada com a expressão \(v=\sqrt{g\cdot h},\) onde g é a aceleração da gravidade local, a razão \(\frac{\lambda_1}{\lambda_2}\) é igual a
\(\frac{h_1}{h_2}\)
\(\frac{\sqrt{h_1\cdot h_2}}{h_1}\)
\(\sqrt{\frac{h_1}{h_2}}\)
\(\sqrt{\frac{h_2}{h_1}}\)
\(\frac{h_2}{h_1}\)
E mais: nota TRI a todo o momento.





