ENEM 2020
Três amigos, André, Bernardo e Carlos, moram em um condomínio fechado de uma cidade. O quadriculado representa a localização das ruas paralelas e perpendiculares. delimitando quadras de mesmo tamanho nesse condomínio, em que nos pontos A, B e C estão localizadas as casas de André, Bernardo e Carlos, respectivamente.
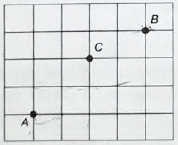
André deseja deslocar-se da sua casa até a casa de Bernardo, sem passar pela casa de Carlos, seguindo ao longo das ruas do condomínio, fazendo sempre deslocamentos para a direita ( \(\rightarrow\) ) ou para cima (\(\uparrow\)), segundo o esquema da figura.
O número de diferentes caminhos que André poderá utilizar para realizar o deslocamento nas condições propostas é
4.
14.
17.
35.
48.
Resolução
Passo a passo da solução:
O problema pede o número de caminhos diferentes para ir do ponto A ao ponto B, movendo-se apenas para a direita (→) ou para cima (↑), sem passar pelo ponto C.
1. Identificar as coordenadas relativas dos pontos:
Vamos considerar o ponto A como a origem (0,0) de um sistema de coordenadas.
- Para ir de A até B, precisamos nos deslocar 4 unidades para a direita e 3 unidades para cima. Portanto, B está na posição (4,3) relativa a A.
- Para ir de A até C, precisamos nos deslocar 2 unidades para a direita e 2 unidades para cima. Portanto, C está na posição (2,2) relativa a A.
2. Calcular o número total de caminhos de A até B:
Qualquer caminho de A(0,0) até B(4,3) consiste em um total de 4 + 3 = 7 movimentos, sendo 4 para a direita (D) e 3 para cima (C). O número total de caminhos é o número de permutações desses 7 movimentos com repetição:
\[ \text{Total de caminhos (A \(\rightarrow\) B)} = P_7^{4,3} = \frac{7!}{4!3!} \]
\[ \frac{7!}{4!3!} = \frac{7 \times 6 \times 5 \times 4!}{4! \times (3 \times 2 \times 1)} = \frac{7 \times 6 \times 5}{6} = 7 \times 5 = 35 \text{ caminhos} \]
3. Calcular o número de caminhos de A até B que passam por C:
Um caminho que passa por C deve ir primeiro de A até C e depois de C até B.
- Caminhos de A(0,0) até C(2,2): São necessários 2 movimentos para a direita (D) e 2 para cima (C), totalizando 2 + 2 = 4 movimentos.
\[ \text{Caminhos (A \(\rightarrow\) C)} = P_4^{2,2} = \frac{4!}{2!2!} = \frac{4 \times 3 \times 2!}{2! \times (2 \times 1)} = \frac{4 \times 3}{2} = 6 \text{ caminhos} \]
- Caminhos de C(2,2) até B(4,3): São necessários (4-2) = 2 movimentos para a direita (D) e (3-2) = 1 movimento para cima (C), totalizando 2 + 1 = 3 movimentos.
\[ \text{Caminhos (C \(\rightarrow\) B)} = P_3^{2,1} = \frac{3!}{2!1!} = \frac{3 \times 2!}{2! \times 1} = 3 \text{ caminhos} \]
O número total de caminhos de A até B passando por C é o produto dos caminhos de A até C pelos caminhos de C até B (Princípio Multiplicativo):
\[ \text{Caminhos (A \(\rightarrow\) C \(\rightarrow\) B)} = \text{Caminhos (A \(\rightarrow\) C)} \times \text{Caminhos (C \(\rightarrow\) B)} = 6 \times 3 = 18 \text{ caminhos} \]
4. Calcular o número de caminhos de A até B que NÃO passam por C:
Para encontrar o número de caminhos que não passam por C, subtraímos o número de caminhos que passam por C do número total de caminhos de A até B:
\[ \text{Caminhos (A \(\rightarrow\) B sem passar por C)} = \text{Total de caminhos (A \(\rightarrow\) B)} - \text{Caminhos (A \(\rightarrow\) C \(\rightarrow\) B)} \]
\[ \text{Caminhos (A \(\rightarrow\) B sem passar por C)} = 35 - 18 = 17 \text{ caminhos} \]
Portanto, o número de diferentes caminhos que André poderá utilizar é 17.
Dicas
Erros Comuns
Revisão de Conceitos
- Permutação com Repetição: Usada para encontrar o número de arranjos distintos de objetos quando alguns deles são idênticos. Para um conjunto de \(n\) objetos com \(n_1\) objetos idênticos do tipo 1, \(n_2\) objetos idênticos do tipo 2, ..., \(n_k\) objetos idênticos do tipo k (onde \(n_1 + n_2 + ... + n_k = n\)), o número de permutações distintas é dado por \( P_n^{n_1, n_2, ..., n_k} = \frac{n!}{n_1! n_2! ... n_k!} \). No problema de caminhos na grade, os 'objetos' são os movimentos (direita ou cima), e as 'repetições' são o número de movimentos em cada direção.
- Contagem de Caminhos em Grade: O número de caminhos mais curtos entre dois pontos (x1, y1) e (x2, y2) em uma grade, movendo-se apenas em direções positivas (direita e cima), é calculado usando permutação com repetição. O número total de movimentos é \( (x2-x1) + (y2-y1) \), com \( (x2-x1) \) movimentos para a direita e \( (y2-y1) \) movimentos para cima.
- Princípio da Subtração (ou Inclusão-Exclusão): Para contar o número de elementos em um conjunto que satisfazem uma condição (não passar por C), podemos contar o número total de elementos (total de caminhos de A para B) e subtrair o número de elementos que *não* satisfazem a condição (caminhos que passam por C).
- Princípio Multiplicativo: Se um evento pode ser dividido em etapas sequenciais e independentes, o número total de maneiras de o evento ocorrer é o produto do número de maneiras de cada etapa ocorrer. Usado aqui para calcular os caminhos que passam por C (etapa A→C seguida da etapa C→B).
Resolver situação-problema envolvendo conhecimentos numéricos.
