clear
FUVEST 1998
Qual das figuras abaixo é um esboço do gráfico da função f(x) = log₂ 2x ?
a
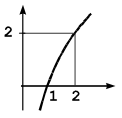
b
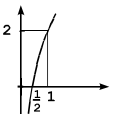
c
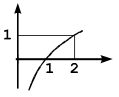
d
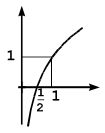
e
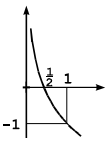
Ver resposta
Ver resposta
Resposta
D
Resolução
Assine a AIO para ter acesso a esta e muitas outras resoluções
Mais de 300.000 questões com resoluções e dados exclusivos disponíveis para alunos AIO.
E mais: nota TRI a todo o momento.
E mais: nota TRI a todo o momento.
Saiba mais
Esta resolução não é pública. Assine a aio para ter acesso a essa resolução e muito mais:
Tenha acesso a simulados reduzidos, mais de 200.000 questões, orientação personalizada,
video aulas, correção de redações e uma equipe sempre disposta a te ajudar.
Tudo isso com acompanhamento TRI em tempo real.
Dicas
expand_more
expand_less
Dicas sobre como resolver essa questão
Erros Comuns
expand_more
expand_less
Alguns erros comuns que estudantes podem cometer ao resolver esta questão
Conceitos chave
Conceitos chave sobre essa questão, que pode te ajudar a resolver questões similares
Estratégia de resolução
Uma estratégia sobre a forma apropriada de se chegar a resposta correta
Transforme seus estudos com a AIO!
Estudantes como você estão acelerando suas aprovações usando nossa plataforma de
AI + aprendizado ativo.
+25 pts
Aumento médio TRI
4x
Simulados mais rápidos
+50 mil
Estudantes

Jairo Thiago
Conheci a plataforma através de uma reportagem e, como gosto de IA, resolvi investir. A quantidade de questões e suas análises foram tão boas que meu número de acertos foi o suficiente para entrar em Medicina na Federal do meu estado, só tenho que agradecer à equipe do AIO pela minha tão sonhada aprovação!

Diana Bittencourt
Não conhecia a AIO em 2022, e em 2023 e o que eu posso dizer sem dúvidas é que foi uma das maiores surpresas no mundo dos estudos. Digo isso porque, por conta dos simulados reduzidos, fazer questões e simuladinhos todo dia virou um hábito gostoso e que me trouxe resultados no ENEM surpreendentes!

Jonas de Souza
As correções de redações e as aulas são bem organizadas e é claro os professores são os melhores com a melhor metodologia de ensino, sem dúvidas contribuiu muito para o aumento de 120 pontos na minha média final!


