clear
ENEM 2010 segunda aplicação
Para verificar e analisar o grau de eficiência de um teste que poderia ajudar no retrocesso de uma doença numa comunidade, uma equipe de biólogos aplicou-o em um grupo de 500 ratos, para detectar a presença dessa doença. Porém, o teste não é totalmente eficaz, podendo existir ratos saudáveis com resultado positivo e ratos doentes com resultado negativo. Sabe-se, ainda, que 100 ratos possuem a doença, 20 ratos são saudáveis com resultado positivo e 40 ratos são doentes com resultado negativo.
Um rato escolhido ao acaso, e verificou-se que o seu resultado deu negativo. A probabilidade de esse rato ser saudável é
a
1/5
b
4/5
c
19/21
d
19/25
e
21/25
Ver resposta
Ver resposta
Resposta
C
Tempo médio
3 min
Resolução
Assine a AIO para ter acesso a esta e muitas outras resoluções
Mais de 300.000 questões com resoluções e dados exclusivos disponíveis para alunos AIO.
E mais: nota TRI a todo o momento.
E mais: nota TRI a todo o momento.
Saiba mais
Esta resolução não é pública. Assine a aio para ter acesso a essa resolução e muito mais:
Tenha acesso a simulados reduzidos, mais de 200.000 questões, orientação personalizada,
video aulas, correção de redações e uma equipe sempre disposta a te ajudar.
Tudo isso com acompanhamento TRI em tempo real.
Dicas
expand_more
expand_less
Dicas sobre como resolver essa questão
Erros Comuns
expand_more
expand_less
Alguns erros comuns que estudantes podem cometer ao resolver esta questão
Conceitos chave
Conceitos chave sobre essa questão, que pode te ajudar a resolver questões similares
Estratégia de resolução
Uma estratégia sobre a forma apropriada de se chegar a resposta correta
Porcentagem de alternativa escolhida por nota TRI
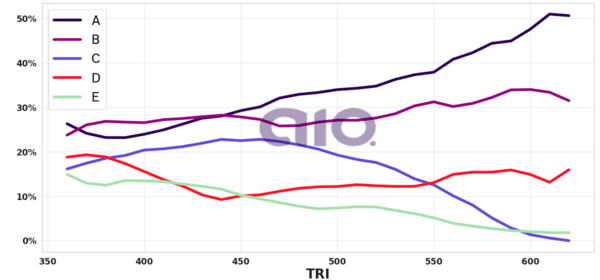
Porcentagem de alternativa escolhida por nota TRI

Transforme seus estudos com a AIO!
Estudantes como você estão acelerando suas aprovações usando nossa plataforma de
AI + aprendizado ativo.
+25 pts
Aumento médio TRI
4x
Simulados mais rápidos
+50 mil
Estudantes

Diana Bittencourt
Não conhecia a AIO em 2022, e em 2023 e o que eu posso dizer sem dúvidas é que foi uma das maiores surpresas no mundo dos estudos. Digo isso porque, por conta dos simulados reduzidos, fazer questões e simuladinhos todo dia virou um hábito gostoso e que me trouxe resultados no ENEM surpreendentes!

Sarah
Neste ano da minha aprovação, a AIO foi a forma perfeita de eu entender meus pontos fortes e fracos, melhorar minha estratégia de prova e, alcançar uma nota excepcional que me permitiu realizar meu objetivo na universidade dos meus sonhos. Só tenho a agradecer à AIO ... pois com certeza não conseguiria sozinha.

Jairo Thiago
Conheci a plataforma através de uma reportagem e, como gosto de IA, resolvi investir. A quantidade de questões e suas análises foram tão boas que meu número de acertos foi o suficiente para entrar em Medicina na Federal do meu estado, só tenho que agradecer à equipe do AIO pela minha tão sonhada aprovação!


