ENEM 2019 segunda aplicação
O boliche é um esporte cujo objetivo é derrubar, com uma bola, uma série de pinos alinhados em uma pista. A professora de matemática organizou um jogo de boliche em que os pinos são garrafas que possuem rótulos com números, conforme mostra o esquema.
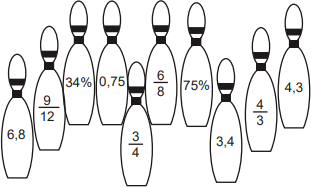
O aluno marca pontos de acordo com a soma das quantidades expressas nos rótulos das garrafas que são derrubadas. Se dois ou mais rótulos representam a mesma quantidade, apenas um deles entra na contagem dos pontos. Um aluno marcou 7,55 pontos em uma jogada. Uma das garrafas que ele derrubou tinha o rótulo 6,8.
A quantidade máxima de garrafas que ele derrubou para obter essa pontuação é igual a
2.
3.
4.
5.
6.
E mais: nota TRI a todo o momento.
Reconhecer, no contexto social, diferentes significados e representações dos números e operações - naturais, inteiros, racionais ou reais.





