clear
ENEM 2019 segunda aplicação
No trapézio isósceles mostrado na figura a seguir, M é o ponto médio do segmento BC, e os pontos P e Q são obtidos dividindo o segmento AD em três partes iguais.
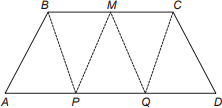
Pelos pontos B, M, C, P e Q são traçados segmentos de reta, determinando cinco triângulos internos ao trapézio, conforme a figura.
A razão entre BC e AD que determina áreas iguais para os cinco triângulos mostrados na figura é
a
1/3
b
2/3
c
2/5
d
3/5
e
5/6
Ver resposta
Ver resposta
Resposta
B
Tempo médio
1 min
Resolução
Assine a AIO para ter acesso a esta e muitas outras resoluções
Mais de 300.000 questões com resoluções e dados exclusivos disponíveis para alunos AIO.
E mais: nota TRI a todo o momento.
E mais: nota TRI a todo o momento.
Saiba mais
Esta resolução não é pública. Assine a aio para ter acesso a essa resolução e muito mais:
Tenha acesso a simulados reduzidos, mais de 200.000 questões, orientação personalizada,
video aulas, correção de redações e uma equipe sempre disposta a te ajudar.
Tudo isso com acompanhamento TRI em tempo real.
Dicas
expand_more
expand_less
Dicas sobre como resolver essa questão
Erros Comuns
expand_more
expand_less
Alguns erros comuns que estudantes podem cometer ao resolver esta questão
Conceitos chave
Conceitos chave sobre essa questão, que pode te ajudar a resolver questões similares
Estratégia de resolução
Uma estratégia sobre a forma apropriada de se chegar a resposta correta
Habilidade
Resolver situação-problema que envolva conhecimentos geométricos de espaço e forma.
Transforme seus estudos com a AIO!
Estudantes como você estão acelerando suas aprovações usando nossa plataforma de
AI + aprendizado ativo.
+25 pts
Aumento médio TRI
4x
Simulados mais rápidos
+50 mil
Estudantes

Rejandson, vestibulando
Eu encontrei a melhor plataforma de estudos para o Enem do Brasil. A AIO é uma plataforma inovadora. Além de estudar com questões ela te dá a TRI assim que você termina.

Mariana Scheffel
AIO foi fundamental para a evolução do meu número de acertos e notas, tanto no ENEM quanto em outros vestibulares, fornecendo os recursos e as ferramentas necessárias para estudar de forma eficaz e melhorar minhas notas.

Jefferson, formando em Medicina
Com a plataforma AIO consegui acertar as 45 questões de ciências humanas no ENEM 2022! Sem dúvidas, obter a nota máxima nessa área, foi imprescindível para ser aprovado em medicina.


