Unioeste 2° Etapa Tarde 2020
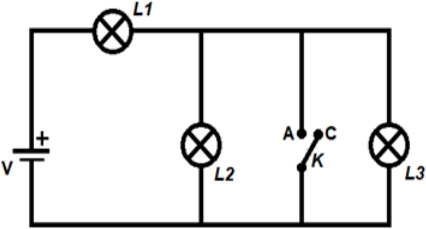
No circuito representado na figura a seguir, L1, L2 e L3 representam lâmpadas incandescentes idênticas, V é uma fonte de tensão contínua e K é uma chave interruptora aberta. Esta chave pode ser fechada efetuando a conexão entre os pontos A e C. A resistência dos fios é desprezível.
Seja B1 o brilho da lâmpada L1; B2 o brilho da lâmpada L2; B3 o brilho da lâmpada L3. Considere as seguintes afirmativas sobre os brilhos das lâmpadas:
I. Quando a chave K está aberta, B2 = B3; B1 > B2; B1 > B3;
II. Quando a chave K está aberta, B1 = B2 = B3;
III. Quando a chave K está fechada, B1 = B2 e B3 = 0, ou seja, L3 está apagada;
IV. Quando a chave K está fechada, B1 está brilhando, B2 = 0 e B3 = 0, ou seja, L2 e L3 estão apagadas.
Estão CORRETAS as afirmativas:
I e III.
I e IV.
II e III.
II e IV.
nenhuma das alternativas.
E mais: nota TRI a todo o momento.





