IFAL 2009/1
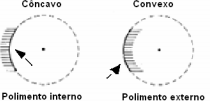
Na figura abaixo, observa-se a representação de espelhos esféricos, que podem ser definidos como uma superfície lisa, de forma esférica, que reflete especularmente a luz. Se a luz estiver se refletindo na superfície interna, trata-se de um espelho côncavo, e se a reflexão acontecer na superfície externa, trata-se de um espelho convexo. Com relação a espelhos esféricos, analise as afirmações a seguir:
Espelhos esféricos
I. Um objeto real é colocado entre o foco e o vértice de um espelho côncavo. Nesta situação, podemos afirmar que a imagem será virtual, direita e maior que o objeto.
II. Exemplos de espelhos convexos são aqueles colocados nos cantos superiores das lojas, para aumentar o campo visual de observação das mesmas. Para esses espelhos, as imagens formadas são sempre menores que o objeto real.
III. Podemos sempre projetar a imagem de um objeto real em uma tela, colocando este objeto a qualquer distância diante de um espelho côncavo.
IV. Com relação a espelhos convexos, existe uma distância específica para a qual não é formada nenhuma imagem (imagem imprópria) de um objeto real.
Estão corretas:
apenas I e II.
apenas III e IV.
apenas I, II e IV.
apenas I, II e III.
I, II, III e IV.
Resolução
Seja um espelho côncavo de distância focal \(f\) e um objeto real colocado a uma distância \(p\) do vértice \(V\).
1. Quando \(0<p<f\) (entre o foco e o vértice), a equação dos espelhos
fornece \(q<0\) (imagem atrás do espelho), logo a imagem é virtual, direita e ampliada.
2. Para espelhos convexos, o raio de curvatura é negativo; qualquer objeto real (\(p>0\)) gera \(q<0\) e módulo de \(q\) < \(p\). Assim, a imagem é sempre virtual, direita e menor que o objeto. É por isso que esses espelhos são instalados em lojas e retrovisores – ampliam o campo visual.
3. Somente imagens reais podem ser projetadas em uma tela. No espelho côncavo isso acontece se \(p>f\). Para \(p<f\) a imagem é virtual e não se projeta. Portanto não se pode projetar a imagem para qualquer distância do objeto.
4. Em espelhos convexos sempre há formação de imagem virtual, independentemente da posição do objeto; não existe distância “imprópria”.
Conclusão: corretas apenas I e II ⇒ alternativa A.
Dicas
Erros Comuns
- Espelhos côncavos: convergentes; imagem depende da posição do objeto.
- Entre V e F: imagem virtual, direita, ampliada.
- Sobre F: imagem imprópria (no infinito).
- Entre F e C: imagem real, invertida, ampliada.
- Sobre C: real, invertida, mesmo tamanho.
- Após C: real, invertida, reduzida. - Espelhos convexos: divergentes; para qualquer posição do objeto a imagem é virtual, direita e reduzida.
- Equação dos espelhos: \(\frac1p+\frac1q=\frac1f\), sinal de Gauss:
- distâncias de objetos reais e raios medidos da esquerda para direita são positivas.
- distâncias de imagens virtuais e raios de espelhos convexos são negativas. - Somente imagens reais podem ser projetadas em tela.
