ENEM 2018 segunda aplicação
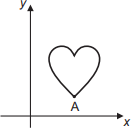
Isometria é uma transformação geométrica que, aplicada a uma figura, mantem as distâncias entre pontos. Duas das transformações isométricas são a reflexão e a rotação. A reflexão ocorre por meio de uma reta chamada eixo. Esse eixo funciona como um espelho, a imagem refletida é o resultado da transformação. A rotação é o “giro” de uma figura ao redor de um ponto chamado centro de rotação. A figura sofreu cinco transformações isométricas, nessa ordem:
1°) Reflexão no eixo x;
2°) Rotação de 90 graus no sentido anti-horário, com centro de rotação no ponto A;
3°) Reflexão no eixo y;
4°) Rotação de 45 graus no sentido horário, com centro de rotação no ponto A;
5°) Reflexão no eixo x.
Disponível em: www.pucsp.br. Acesso em: 2 ago. 2012.
Qual a posição final da figura?




Resolução
Para resolver esta questão, devemos aplicar cada uma das cinco transformações isométricas na ordem dada, começando pela figura inicial.
A figura inicial é um coração com a ponta inferior marcada como ponto A, localizado sobre o eixo x positivo. O corpo do coração está no primeiro quadrante.

1ª Transformação: Reflexão no eixo x.
O eixo x funciona como um espelho. Pontos \((x, y)\) são transformados em \((x, -y)\). Como o ponto A está sobre o eixo x (sua coordenada y é 0), ele permanece na mesma posição. A figura, que estava acima do eixo x, é refletida para baixo, ficando de cabeça para baixo, com o corpo principal no quarto quadrante e a ponta A ainda sobre o eixo x positivo.2ª Transformação: Rotação de 90 graus no sentido anti-horário, com centro de rotação no ponto A.
O centro de rotação é o ponto A. A figura (agora de cabeça para baixo) gira 90° no sentido anti-horário em torno de A. A figura que apontava para baixo (ao longo do eixo y negativo, relativamente a A) passa a apontar para a esquerda (ao longo do eixo x negativo, relativamente a A). Como A está no eixo x positivo, a figura agora aponta para cima (direção do eixo y positivo), e o corpo do coração fica à esquerda de A, principalmente no segundo quadrante. O ponto A permanece no eixo x positivo.3ª Transformação: Reflexão no eixo y.
O eixo y funciona como um espelho. Pontos \((x, y)\) são transformados em \((-x, y)\). O ponto A, que estava no eixo x positivo, é refletido para o eixo x negativo. A figura, que apontava para cima com o corpo à esquerda de A, é refletida horizontalmente. Ela continua apontando para cima, mas agora o corpo do coração fica à direita de A, principalmente no primeiro quadrante. O ponto A está agora sobre o eixo x negativo.4ª Transformação: Rotação de 45 graus no sentido horário, com centro de rotação no ponto A.
O centro de rotação é o ponto A (agora no eixo x negativo). A figura (apontando para cima) gira 45° no sentido horário em torno de A. O sentido horário a partir da direção "para cima" (eixo y positivo) é em direção ao eixo x positivo. Portanto, a figura passa a apontar na diagonal, para cima e para a direita, formando um ângulo de 45° com o eixo y (ou 45° com o eixo x negativo no sentido horário). O ponto A permanece no eixo x negativo.5ª Transformação: Reflexão no eixo x.
Novamente, o eixo x funciona como um espelho. Pontos \((x, y)\) são transformados em \((x, -y)\). O ponto A, que está sobre o eixo x negativo, permanece na mesma posição. A figura, que apontava diagonalmente para cima e para a direita, é refletida verticalmente para baixo. Ela passa a apontar diagonalmente para baixo e para a direita. O corpo principal fica no quarto quadrante. O ponto A permanece no eixo x negativo.
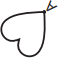
A posição final da figura é com o ponto A sobre o eixo x negativo e o coração apontando diagonalmente para baixo e para a direita.
Comparando com as opções:
- A: Ponto A no eixo y positivo. Incorreto.
- B: Ponto A no eixo x positivo. Incorreto.
- C: Ponto A no eixo x negativo, figura aponta para baixo e direita. Correto.
- D: Ponto A no eixo y negativo. Incorreto.
- E: Ponto A no eixo x negativo, figura aponta para baixo e esquerda. Incorreto.
Portanto, a posição final da figura é a mostrada na opção C.

Dicas
Erros Comuns
Esta questão aborda Transformações Geométricas Isométricas no plano cartesiano.
- Isometria: Uma transformação geométrica que preserva as distâncias entre os pontos e, consequentemente, a forma e o tamanho da figura. As principais isometrias são translação, rotação e reflexão.
- Reflexão: Uma transformação que "espelha" a figura em relação a uma reta chamada eixo de reflexão. Na reflexão em relação ao eixo x, um ponto \((x, y)\) se torna \((x, -y)\). Na reflexão em relação ao eixo y, um ponto \((x, y)\) se torna \((-x, y)\).
- Rotação: Uma transformação que "gira" a figura em torno de um ponto fixo (centro de rotação) por um determinado ângulo e em um sentido específico (horário ou anti-horário). A rotação preserva a forma e o tamanho, mas muda a orientação da figura.
Identificar características de figuras planas ou espaciais.





