ENEM 2020 segunda aplicação
Embora a civilização maia já estivesse em declínio na época da chegada dos espanhóis à América, seu desenvolvimento em vários campos da ciência, em especial, na matemática e na astronomia, era notável. Eles possuíam um sistema numérico avançado e diferente do sistema decimal utilizado pelas sociedades modernas.
A imagem representa o sistema de numeração maia, que consistia em 20 símbolos representando os números de 0 a 19.
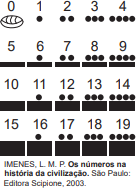
O zero era representado por uma espécie de tigela e todo número inteiro entre 19 e 360 era escrito em uma coluna vertical com duas figuras, na qual a superior representava a quantidade de grupos de 20 unidades e a inferior, a quantidade de unidades. O número era lido de cima para baixo e obtido somando-se as quantidades representadas. Por exemplo:
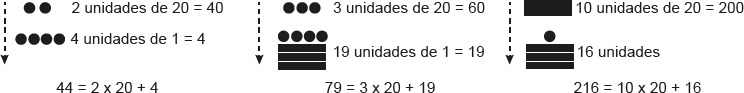
O número 359 é representado, no sistema de numeração maia, como





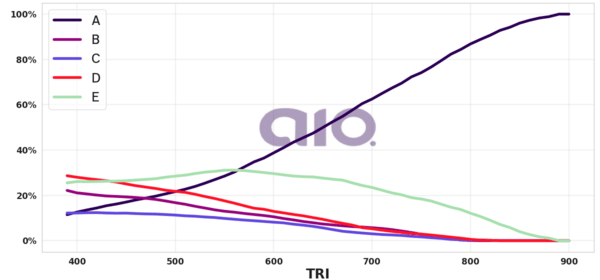
E mais: nota TRI a todo o momento.
Reconhecer, no contexto social, diferentes significados e representações dos números e operações - naturais, inteiros, racionais ou reais.