ENEM 2010 segunda aplicação
Resolução
A questão descreve uma corrida de regularidade, onde o objetivo é manter um tempo o mais próximo possível de um tempo alvo definido pela organização. A equipe vencedora é aquela que demonstra maior regularidade, ou seja, cujos tempos individuais dos participantes variam menos em torno do tempo alvo.
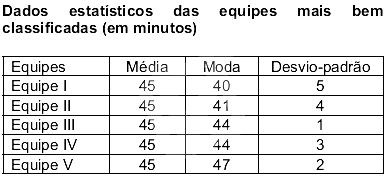
O tempo alvo fornecido pelos organizadores foi de 45 minutos por prova. A tabela apresenta dados estatísticos para as cinco melhores equipes:
- Média: O tempo médio de cada equipe.
- Moda: O tempo que ocorreu com maior frequência dentro de cada equipe.
- Desvio-padrão: Uma medida estatística que indica o quão dispersos estão os tempos individuais dos participantes em relação à média da equipe.
Observamos na tabela que todas as cinco equipes têm uma média de 45 minutos, que é exatamente o tempo alvo. Isso significa que, em média, todas as equipes atingiram o objetivo. No entanto, para determinar a equipe campeã (a mais regular), precisamos verificar qual delas teve os tempos mais consistentes, ou seja, mais próximos da média de 45 minutos.
A medida estatística que quantifica a regularidade ou a dispersão dos dados em torno da média é o desvio-padrão. Quanto menor o desvio-padrão, mais agrupados estão os dados em torno da média, indicando maior regularidade. Quanto maior o desvio-padrão, mais espalhados estão os tempos, indicando menor regularidade.
Analisando os desvios-padrão de cada equipe na tabela:
- Equipe I: Desvio-padrão = 5
- Equipe II: Desvio-padrão = 4
- Equipe III: Desvio-padrão = 1
- Equipe IV: Desvio-padrão = 3
- Equipe V: Desvio-padrão = 2
A Equipe III possui o menor desvio-padrão (1). Isso significa que os tempos dos participantes dessa equipe foram os mais consistentes e mais próximos da média de 45 minutos.
Portanto, a equipe campeã, por ser a mais regular, foi a Equipe III.
Dicas
Erros Comuns
Para resolver esta questão, é fundamental entender os seguintes conceitos de estatística descritiva:
- Média Aritmética: É a soma de todos os valores dividida pelo número total de valores. Indica o valor central em torno do qual os dados tendem a se agrupar. No problema, todas as equipes têm média 45 minutos.
- Moda: É o valor que aparece com maior frequência em um conjunto de dados.
- Desvio-Padrão: É uma medida da dispersão ou variabilidade dos dados em relação à média. Um desvio-padrão baixo indica que os dados estão concentrados perto da média (alta regularidade). Um desvio-padrão alto indica que os dados estão mais espalhados (baixa regularidade).
Em problemas de regularidade, onde se busca a maior consistência ou a menor variação em torno de um valor alvo (que aqui coincide com a média), o desvio-padrão é a medida decisiva. A equipe com o menor desvio-padrão é a mais regular.