UnB 2010/1
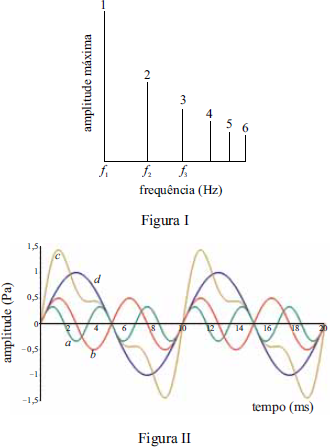
Em música, frequência fundamental é a menor frequência componente da série harmônica de um som. Os harmônicos de uma onda são múltiplos inteiros da respectiva frequência fundamental. Por exemplo, se a frequência fundamental é f, os harmônicos têm frequências 2f, 3f, 4f etc. As amplitudes variam, mas, de modo geral, quanto mais elevado for o harmônico, menor será a sua amplitude. A figura I mostra o gráfico da amplitude máxima versus frequência de um som composto por uma frequência fundamental f1 e seus harmônicos. A figura II ilustra a variação de pressão, em Pa, produzida por várias ondas senoidais em função do tempo, em ms, entre elas, as três, de frequências f1, f2 e f3, indicadas na figura I.
A partir dessas informações e com auxílio das figuras I e II acima, julgue o item.
Se a função y = f(t) = αsen( βt) for uma representação da onda d, em que t seja expresso em milissegundos, é correto afirmar que \(\frac{\alpha}{\beta}<0,0016\) Pa•s.
CERTO.
ERRADO.
Tudo com nota TRI em tempo real
