Ministério da Defesa - Aeronáutica 2023
Nas questões de Física, quando necessário, utilize:
• π = 3,0
• 1 cal = 4,2 J
• 1 mês = 30 dias
• g = 10 m/s2
Duas ondas periódicas harmônicas dadas pelas equações de onda y1 e y2, em unidades do sistema internacional, apresentadas abaixo, propagam-se em uma corda homogênea de comprimento L = 1 m.
y1 (x,t) = − (0,10) cos[2πx+1600πt]
y2 (x,t) = + (0,10) cos[2πx-1600πt]
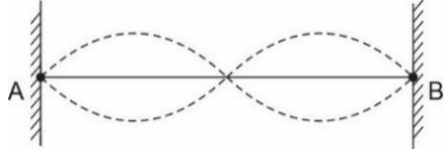
A corda possui duas extremidades fixas em paredes rígidas nos pontos A e B de acordo com o diagrama abaixo.
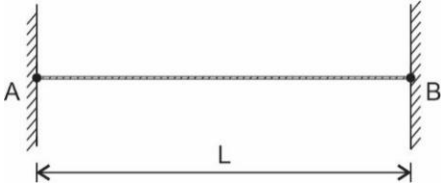
A superposição dessas ondas estabelece o fenômeno de interferência conhecido como ondas estacionárias.
Considere que a velocidade de propagação das ondas na corda seja constante e que não ocorra nenhum tipo de dissipação energética no sistema.
Nessas condições, a equação da onda estacionária resultante na corda, yR (x,t), e a representação do respectivo harmônico estabelecido são melhor apresentadas na opção
yR (x,t)=(0,1) sen [2πx] cos [2πx-1600πt]
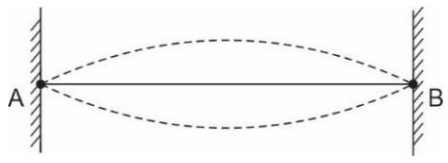
yR (x,t)=(0,2) sen [4πx] sen [2πx-1600πt]
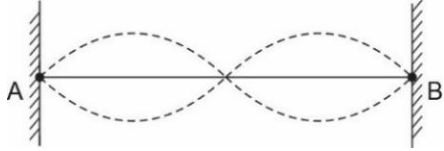
yR (x,t)=(0,1) sen [1600πx] sen [2πx-1600πt]
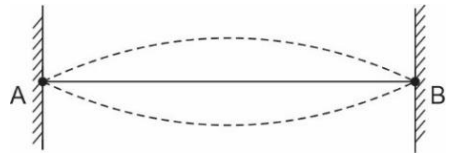
yR (x,t)=(0,2) sen [2πx] sen [1600πt]
E mais: nota TRI a todo o momento.





