AFA 2020
Considere um dioptro plano constituído de dois meios homogêneos e transparentes de índices de refração n1 = 1 e n2 = 4/3, separados por uma superfície S perfeitamente plana.
No meio de índice de refração n1 encontra-se um objeto pontual B, distante d, da superfície S, assim como, no outro meio encontra-se um objeto idêntico A, também distante d, da superfície do dioptro como mostra a figura abaixo.
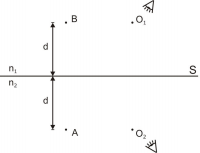
A imagem A1 de A é vista por um observador O1 que se encontra no meio n1; por sua vez, a imagem B1 de B é vista por um observador O2 que se encontra no meio n2.
O dioptro plano é considerado perfeitamente estigmático e os raios que saem de A e B são pouco inclinados em relação à vertical que passa pelos dois objetos.
Considere que A e B sejam aproximados verticalmente da superfície S de uma distância d/2 e suas novas imagens, A2 e B2, respectivamente, sejam vistas pelos observadores O1 e O2.
Nessas condições, a razão dA/dB entre as distâncias, dA e dB, percorridas pelas imagens dos objetos A e B, é
9/16
3/8
3/4
8/3
E mais: nota TRI a todo o momento.





