Secretaria da Educação e do Esporte do Paraná 2023

Analise o texto abaixo para responder às questões de 16 a 18.

Devido ao recorte dos conteúdos escolares é comum que os experimentos didáticos de lançamento sejam realizados com esferas deslocando-se em calhas considerando apenas o movimento translacional, como se realizassem um deslizamento puro. Entretanto, em decorrência dos efeitos do atrito entre a esfera e a calha, o movimento rotacional não pode ser desprezado. Consideremos o caso de uma calha ajustada para a realização de um lançamento horizontal, ou seja, permite que a esfera seja abandonada de determinada altura e ao final a esfera é lançada horizontalmente após um trecho horizontal de calha. Se o movimento neste caso fosse um deslizamento puro a velocidade do centro de massa (v_CM) no momento do lançamento seria dado pela relação:

\(V_{CM}=\sqrt{2gh}\)

sendo h o deslocamento vertical do centro de massa (CM) da esfera durante o movimento na rampa.

Por outro lado, se o movimento fosse de rolamento puro nas bordas da calha a velocidade do centro de massa no lançamento pode ser modelado pela seguinte relação:

\(V_{CM}=\sqrt{2gh}\ \sqrt{1-\frac{2}{7-5\left(L⁄D\right)^2}}\)

sendo D o diâmetro da esfera e L a largura da calha, como representado na figura 1:

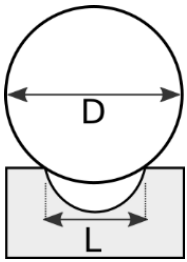
Figura 1. Representação da esfera em contato com a calha

Neste modelo, a resistência do ar está sendo desprezada.

Considere que A_D é o alcance para o deslizamento puro, que A_R é o alcance para o rolamento puro nas condições apresentadas no texto de suporte, que H é o deslocamento vertical do centro de massa após o lançamento e que a largura da calha é muito menor que o diâmetro da esfera (L << D). Assinale a alternativa que representa a expressão da diferença entre o alcance nas duas condições (A_D - A_R) e o valor aproximado dessa diferença se h = 35 cm e H = 1,0 m. Caso necessite, utilize as seguintes aproximações \(\sqrt{2}\) = 𝟏, 𝟒,\(\sqrt{5}\) = 𝟐, 𝟐 e \(\sqrt{7}\) = 𝟐, 𝟔.