ENEM 2021 segunda aplicação
Até a Copa de 2010, apenas sete jogadores haviam conseguido o feito de marcar 8 ou mais gols em uma mesma edição da Copa do Mundo. O quadro apresenta os anos das edições da copa nas quais ocorreram esses feitos, quais foram os jogadores que os realizaram e os respectivos números de gols marcados por cada um deles.
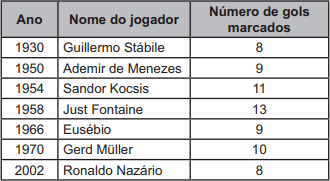
Para facilitar a análise sobre a quantidade de gols marcados por esses artilheiros nas referidas copas, foi calculada a mediana da distribuição dos números de gols marcados por eles nas sete copas especificadas no quadro.
A mediana dessa distribuição é igual a
9,0.
9,7.
10,0.
10,2.
13,0.
Resolução
Passo a passo da solução:
-
Identificar os dados: A questão pede a mediana do número de gols marcados pelos jogadores listados na tabela. Os números de gols são: 8, 9, 11, 13, 9, 10, 8.
-
Organizar os dados: Para calcular a mediana, precisamos primeiro ordenar os dados em ordem crescente (ou decrescente). Vamos ordená-los em ordem crescente:
\( \{8, 8, 9, 9, 10, 11, 13\} \)
-
Encontrar a mediana: A mediana é o valor central de um conjunto de dados ordenado. Como temos 7 valores (um número ímpar de dados), a mediana será o valor que está exatamente no meio da lista ordenada.
A posição do termo central em um conjunto com \( n \) elementos ímpares é dada por \( \frac{n+1}{2} \). Neste caso, \( n = 7 \), então a posição da mediana é \( \frac{7+1}{2} = \frac{8}{2} = 4 \).
O 4º valor na lista ordenada \( \{8, 8, 9, \mathbf{9}, 10, 11, 13\} \) é 9.
-
Concluir: Portanto, a mediana da distribuição dos números de gols marcados é 9.
Resposta: A mediana dessa distribuição é igual a 9,0.
Dicas
Erros Comuns
Revisão de Conceito: Mediana
A mediana é uma medida de tendência central que representa o valor do meio de um conjunto de dados quando estes estão ordenados em ordem crescente ou decrescente.
- Se o número de dados (n) for ímpar: A mediana é o valor que ocupa a posição central, ou seja, a posição \( \frac{n+1}{2} \) após ordenar os dados.
- Se o número de dados (n) for par: A mediana é a média aritmética dos dois valores centrais, que ocupam as posições \( \frac{n}{2} \) e \( \frac{n}{2} + 1 \) após ordenar os dados.
Nesta questão, temos 7 valores (número ímpar), então a mediana é o valor na posição \( \frac{7+1}{2} = 4ª \) posição da lista ordenada.
Calcular medidas de tendência central ou de dispersão de um conjunto de dados expressos em uma tabela de freqüências de dados agrupados (não em classes) ou em gráficos.