PUC-PR Verão 2013
As pirâmides \(P1,\ P2\ e\ P3,\) representadas na figura a seguir, são as três primeiras de uma sequência infinita \((P1,\ P2,\ P3,\ ...)\) de pirâmides regulares. As sequências \((h1,\ h2,\ h3,\ ...)\ e\ (a1,\ a2,\ a3,\ ...)\) são progressões geométricas, onde hn e an representam, nessa ordem, as medidas da altura e da aresta da base da pirâmide Pn, n ∈ ℕ*. Considere ainda Vn como sendo o volume da pirâmide Pn.
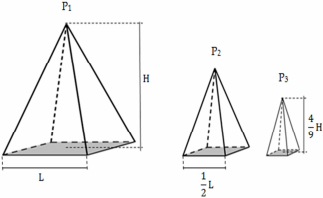
Analise as afirmações a seguir e marque a alternativa CORRETA.
\(I.\ h_2=\frac {2}{3}H\)
\(II.\ \frac {V_2}{V_1}=\( \frac {2}{3}\) ^3\)
\(III.\ V_4= \frac {L^2.H}{648}\)
\(IV.\ V_1+V_2+V_3+...= \frac {6}{5}V_1\)
V. Se \(L=12\ cm\ e\ H=8\ cm,\) então a pirâmide P1 tem \(384\ cm^2\) de área total.
Apenas as afirmações I, III, IV e V são verdadeiras.
Apenas as afirmações I, II e III são verdadeiras.
Apenas as afirmações III e IV são verdadeiras.
Apenas as afirmações I e V são verdadeiras.
Apenas as afirmações II, III e IV são verdadeiras.
E mais: nota TRI a todo o momento.





