clear
UEL 2013
As lâmpadas de LED (Light Emissor Diode) estão substituindo progressivamente as lâmpadas fluorescentes e representam um avanço tecnológico nas formas de conversão de energia elétrica em luz. A tabela, a seguir, compara as características dessas lâmpadas.
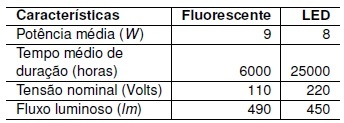
Com relação à eficácia luminosa, que representa a relação entre o fluxo luminoso e a potência do dispositivo, Lumen por Watt (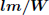
), considere as afirmativas a seguir.
I. A troca da lâmpada fluorescente pela de LED ocasionará economia de 80% de energia.
II. A eficácia luminosa da lâmpada de LED é de 56, 25.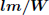
III. A razão entre as correntes elétricas que passam pela lâmpada fluorescente e pela lâmpada de LED, nessa ordem, é de 2, 25.
IV. O consumo de energia elétrica de uma lâmpada de LED durante o seu tempo médio de duração é de 200 kWh.
Assinale a alternativa correta.
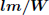), considere as afirmativas a seguir.I. A troca da lâmpada fluorescente pela de LED ocasionará economia de 80% de energia.
II. A eficácia luminosa da lâmpada de LED é de 56, 25
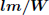.III. A razão entre as correntes elétricas que passam pela lâmpada fluorescente e pela lâmpada de LED, nessa ordem, é de 2, 25.
IV. O consumo de energia elétrica de uma lâmpada de LED durante o seu tempo médio de duração é de 200 kWh.
Assinale a alternativa correta.
a
Somente as afirmativas I e II são corretas.
b
Somente as afirmativas I e IV são corretas.
c
Somente as afirmativas III e IV são corretas.
d
Somente as afirmativas I, II e III são corretas.
e
Somente as afirmativas II, III e IV são corretas.
Ver resposta
Ver resposta
Resposta
E
Resolução
Assine a AIO para ter acesso a esta e muitas outras resoluções
Mais de 300.000 questões com resoluções e dados exclusivos disponíveis para alunos AIO.
E mais: nota TRI a todo o momento.
E mais: nota TRI a todo o momento.
Saiba mais
Esta resolução não é pública. Assine a aio para ter acesso a essa resolução e muito mais:
Tenha acesso a simulados reduzidos, mais de 200.000 questões, orientação personalizada,
video aulas, correção de redações e uma equipe sempre disposta a te ajudar.
Tudo isso com acompanhamento TRI em tempo real.
Dicas
expand_more
expand_less
Dicas sobre como resolver essa questão
Erros Comuns
expand_more
expand_less
Alguns erros comuns que estudantes podem cometer ao resolver esta questão
Conceitos chave
Conceitos chave sobre essa questão, que pode te ajudar a resolver questões similares
Estratégia de resolução
Uma estratégia sobre a forma apropriada de se chegar a resposta correta
Transforme seus estudos com a AIO!
Estudantes como você estão acelerando suas aprovações usando nossa plataforma de
AI + aprendizado ativo.
+25 pts
Aumento médio TRI
4x
Simulados mais rápidos
+50 mil
Estudantes
Jefferson, formando em Medicina
Com a plataforma AIO consegui acertar as 45 questões de ciências humanas no ENEM 2022! Sem dúvidas, obter a nota máxima nessa área, foi imprescindível para ser aprovado em medicina.
Diana Bittencourt
Não conhecia a AIO em 2022, e em 2023 e o que eu posso dizer sem dúvidas é que foi uma das maiores surpresas no mundo dos estudos. Digo isso porque, por conta dos simulados reduzidos, fazer questões e simuladinhos todo dia virou um hábito gostoso e que me trouxe resultados no ENEM surpreendentes!
Débora Adelina
O que mais gostei foi a forma como a plataforma seleciona matérias em que tenho mais dificuldade, ajudando a focar no que realmente preciso de atenção. Ainda não consegui minha aprovação, mas contarei com a AIO por mais um ano pois a plataforma me aproximou desse objetivo tornando meus estudos mais direcionados!