ENEM 2010 segunda aplicação
Resolução
Passo a passo da solução:
-
Compreender a relação entre Resistência e Condutividade:
O enunciado informa que a resistência elétrica (R) de um fio depende de suas dimensões (comprimento L e área de seção reta A) e da condutividade (σ) do material. Embora a fórmula não seja explicitamente fornecida, a relação fundamental é dada por \( R = \frac{L}{\sigma A} \). Esta fórmula mostra que, para um fio com comprimento L e área A constantes, a resistência R é inversamente proporcional à condutividade σ. Ou seja, quanto maior a condutividade, menor a resistência.
-
Identificar o objetivo:
A questão pede para encontrar o material que resulta na *menor* resistência elétrica, mantendo as dimensões geométricas (L e A) constantes.
-
Aplicar a relação inversa:
Como queremos a menor resistência (R) e sabemos que \( R \propto \frac{1}{\sigma} \), precisamos procurar o material com a *maior* condutividade (σ) na tabela fornecida.
-
Analisar a Tabela de Condutividade:
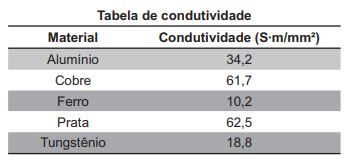
A tabela apresenta os seguintes valores de condutividade (em S·m/mm²):
- Alumínio: 34,2
- Cobre: 61,7
- Ferro: 10,2
- Prata: 62,5
- Tungstênio: 18,8
-
Identificar o maior valor de condutividade:
Comparando os valores, observamos que a Prata possui a maior condutividade:
\( \sigma_{Prata} = 62,5 \text{ S·m/mm²} \)
Este valor é maior que os demais (Cobre: 61,7; Alumínio: 34,2; Tungstênio: 18,8; Ferro: 10,2).
-
Concluir:
Como a Prata tem a maior condutividade, um fio feito de Prata (mantendo L e A constantes) terá a menor resistência elétrica.
-
Selecionar a alternativa correta:
A alternativa que corresponde à Prata é a E.
Dicas
Erros Comuns
Revisão de Conceitos
Resistência Elétrica (R): É a oposição que um material oferece à passagem de corrente elétrica. Sua unidade no SI é o Ohm (Ω).
Condutividade Elétrica (σ): É uma medida da capacidade de um material conduzir corrente elétrica. É o inverso da resistividade (ρ). Quanto maior a condutividade, melhor o material conduz eletricidade. Sua unidade no SI é Siemens por metro (S/m), mas na tabela foi usada S·m/mm².
Resistividade Elétrica (ρ): É uma propriedade intrínseca do material que quantifica sua oposição à corrente elétrica. \( \rho = 1/\sigma \). Sua unidade no SI é Ohm·metro (Ω·m).
Segunda Lei de Ohm: Relaciona a resistência (R) de um condutor com suas dimensões geométricas e o material de que é feito. A fórmula é: \[ R = \rho \frac{L}{A} \] Onde L é o comprimento e A é a área da seção transversal. Usando a condutividade (\( \sigma = 1/\rho \)), a fórmula se torna: \[ R = \frac{1}{\sigma} \frac{L}{A} = \frac{L}{\sigma A} \] Esta fórmula mostra que a resistência é diretamente proporcional ao comprimento (L) e inversamente proporcional à área da seção transversal (A) e à condutividade (σ).