ENEM 2018 segunda aplicação
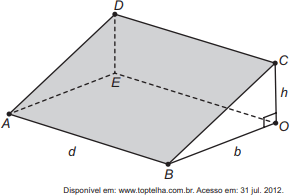
À inclinação de um telhado depende do tipo e da marca das telhas escolhidas. A figura é o esboço do telhado da casa de um específico proprietário. As telhas serão apoiadas sobre a superfície quadrada plana ABCD, sendo BOC um triângulo retângulo em O. Sabe-se que h é a altura do telhado em relação ao forro da casa (a figura plana ABOE), b = 10 é o comprimento do segmento OB, e d é a largura do telhado (segmento AB), todas as medidas dadas em metro.
Sabe-se que, em função do tipo de telha escolhida pelo proprietário, a porcentagem i de inclinação ideal do telhado, descrita por meio da relação \(i = \frac{h \times 100}{b}\), é de 40%, e que a expressão que determina o número N de telhas necessárias na cobertura é dada por N = d2 x 10,5, Além disso, essas telhas são vendidas somente em milheiros.
O proprietário avalia ser fundamental respeitar a inclinação ideal informada pelo fabricante, por isso argumenta ser necessário adquirir a quantidade minima de telhas correspondente a
um milheiro.
dois milheiros.
três milheiros.
seis milheiros.
oito milheiros.
Resolução
O problema pede a quantidade mínima de milheiros de telhas a serem adquiridos para cobrir um telhado, respeitando a inclinação ideal e sabendo como o número de telhas é calculado e como elas são vendidas.
1. Calcular a altura \(h\) do telhado:
A inclinação ideal \(i\) é dada por \(i = \frac{h \times 100}{b}\). Foi informado que \(i = 40\%\) e \(b = 10\) metros.
Substituindo os valores na fórmula:
\[ 40 = \frac{h \times 100}{10} \]
Multiplicando ambos os lados por 10:
\[ 40 \times 10 = h \times 100 \]
\[ 400 = 100h \]
Dividindo ambos os lados por 100:
\[ h = \frac{400}{100} = 4 \text{ metros} \]
2. Calcular o comprimento \(BC\):
A figura mostra que o triângulo \(BOC\) é retângulo em \(O\). Temos \(OB = b = 10\) m e \(OC = h = 4\) m. O segmento \(BC\) é a hipotenusa desse triângulo. Pelo Teorema de Pitágoras:
\[ BC^2 = OB^2 + OC^2 \]
\[ BC^2 = 10^2 + 4^2 \]
\[ BC^2 = 100 + 16 \]
\[ BC^2 = 116 \]
3. Calcular a largura \(d\) e a área da superfície \(ABCD\):
O enunciado informa que a superfície \(ABCD\) é quadrada. Portanto, todos os seus lados são iguais. A largura \(d\) é o comprimento do segmento \(AB\). Como \(ABCD\) é um quadrado, temos \(AB = BC\).
Logo, \(d = BC\). Elevando ao quadrado, temos \(d^2 = BC^2\).
\[ d^2 = 116 \text{ metros quadrados} \]
Note que \(d^2\) representa a área da superfície quadrada \(ABCD\) que será coberta pelas telhas.
4. Calcular o número \(N\) de telhas necessárias:
A expressão para o número de telhas é \(N = d^2 \times 10,5\).
Substituindo \(d^2 = 116\):
\[ N = 116 \times 10,5 \]
Podemos calcular \(116 \times 10,5\) como \(116 \times (10 + 0,5) = (116 \times 10) + (116 \times 0,5) = 1160 + 58\):
\[ N = 1218 \text{ telhas} \]
5. Determinar a quantidade mínima de milheiros:
As telhas são vendidas somente em milheiros (lotes de 1000). O proprietário precisa de 1218 telhas.
Como 1 milheiro (1000 telhas) não é suficiente, ele precisará comprar o próximo múltiplo de 1000 que seja maior ou igual a 1218.
Portanto, ele deve adquirir 2000 telhas.
Isso corresponde a 2 milheiros.
Dicas
Erros Comuns
Para resolver esta questão, são necessários os seguintes conceitos:
- Porcentagem: Entender como calcular um valor a partir de uma porcentagem dada e uma fórmula (\(i = \frac{h \times 100}{b}\)).
- Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos (\(a^2 = b^2 + c^2\)). Utilizado para encontrar o comprimento \(BC\) no triângulo \(BOC\).
- Propriedades de um Quadrado: Saber que um quadrado tem todos os lados iguais. Isso permite relacionar \(d\) (lado \(AB\)) com \(BC\).
- Cálculo de Área: Implicitamente, \(d^2\) é a área da superfície quadrada \(ABCD\).
- Interpretação de Problemas e Unidades: Compreender como as informações se conectam e como as unidades (metros, porcentagem, número de telhas, milheiros) são usadas.
- Raciocínio Lógico para Compra: Entender que, como as telhas são vendidas em lotes (milheiros), é necessário comprar uma quantidade igual ou superior à necessidade calculada, arredondando para cima para o próximo milheiro.
Utilizar conhecimentos geométricos de espaço e forma na seleção de argumentos propostos como solução de problemas do cotidiano.





