Instituto Federal de Educação, Ciência e Tecnologia Farroupilha 2016
A figura abaixo apresenta um diagrama unifilar de um sistema de potência de três barras.
Sistema de potência com três barras
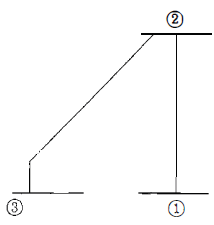
Considerando que as admitâncias série das linhas entre as barras 1 e 2, e entre as barras 2 e 3, são denotadas, respectivamente, por \(y_{12}^{se}\) e \(y_{23}^{se}\), e que as admitâncias em derivação destas mesmas linhas são denotadas, respectivamente, por \(y_{12}^{sh}\) e \(y_{23}^{sh}\). A matriz que representa a matriz admitância de barras deste sistema é:
\( \begin{bmatrix} y_{12}^{se}+y_{12}^{sh} & -y_{12}^{se} & 0 \\ -y_{12}^{se} & y_{12}^{se}+y_{23}^{se}+y_{23}^{sh}+y_{12}^{sh} & -y_{23}^{se} \\ 0 & -y_{23}^{se} & y_{23}^{se}+y_{23}^{sh} \\ \end{bmatrix}\)
\( \begin{bmatrix} y_{12}^{se}+y_{12}^{sh} & y_{12}^{se} & 0 \\ y_{12}^{se} & y_{12}^{se}+y_{23}^{se}+y_{23}^{sh}+y_{12}^{sh} & y_{23}^{se} \\ 0 & y_{23}^{se} & y_{23}^{se}+y_{23}^{sh} \\ \end{bmatrix}\)
\( \begin{bmatrix} y_{12}^{se}+y_{12}^{sh} & -y_{12}^{se}-y_{12}^{sh} & 0 \\ -y_{12}^{se}-y_{12}^{sh} & y_{12}^{se}+y_{23}^{se}+y_{23}^{sh}+y_{12}^{sh} & -y_{23}^{se}-y_{23}^{sh} \\ 0 & -y_{23}^{se}-y_{23}^{sh} & y_{23}^{se}+y_{23}^{sh} \\ \end{bmatrix}\)
\( \begin{bmatrix} y_{12}^{se}+y_{12}^{sh} & y_{12}^{se}+y_{12}^{sh} & 0 \\ y_{12}^{se}+y_{12}^{sh} & y_{12}^{se}+y_{23}^{se}+y_{23}^{sh}+y_{12}^{sh} & y_{23}^{se}+y_{23}^{sh} \\ 0 & y_{23}^{se}+y_{23}^{sh} & y_{23}^{se}+y_{23}^{sh} \\ \end{bmatrix}\)
\( \begin{bmatrix} y_{12}^{se}-y_{12}^{sh} & y_{12}^{se} & 0 \\ y_{12}^{se} & y_{12}^{se}+y_{23}^{se}-y_{23}^{sh}-y_{12}^{sh} & y_{23}^{se} \\ 0 & y_{23}^{se} & y_{23}^{se}-y_{23}^{sh} \\ \end{bmatrix}\)
E mais: nota TRI a todo o momento.





