EMESCAM 2013/2
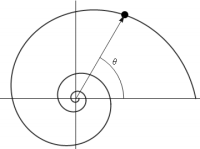
A espiral logarítmica (ver figura a seguir) é uma forma geométrica descrita pela equação \(ln\left(\frac{r}{R}\right)=\frac{\theta}{tan\left(\alpha\right)},\) onde R é o raio associado a \(\theta = 0,\) r é a distância da origem até um ponto da curva em função de θ que é medido em radianos, ln é o logaritmo natural, tan é a função tangente e α é um ângulo. Essa espiral aparece de forma aproximada com grande frequência na natureza, por exemplo, nas cascas de caramujos, furacões e até no formato de galáxias.
Supondo valores constantes para α e R, assinale a alternativa abaixo que expressa corretamente o valor final de r em função do seu valor inicial \(r_0 ,\) caso o ângulo θ dobre de valor:
\(r_f=\frac{2r_0}{R}.\)
\(r_f=\frac{r_0}{2R}.\)
\(r_f=\frac{r_0\ ^2}{2R }.\)
\(r_f=\frac{r_0\ ^2}{R }.\)
\(r_f=\frac{2r_0\ ^2}{R }.\)
E mais: nota TRI a todo o momento.





